Leetcode - 968：监控二叉树

鉴于你校人均OI背景…本萌新还是需要好好补充算法知识XD

968. 监控二叉树（困难）

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

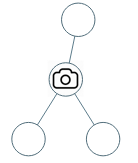
示例 1：

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
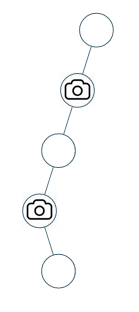
示例 2：

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-cameras
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

仔细想想，对于一个结点是否需要安装摄像头，其实是由其子树的状态来决定的，那么我们可以使用动态规划算法

解法：递归 + 深度优先搜索（DFS） + 动态规划（DP）

大概如下图所示：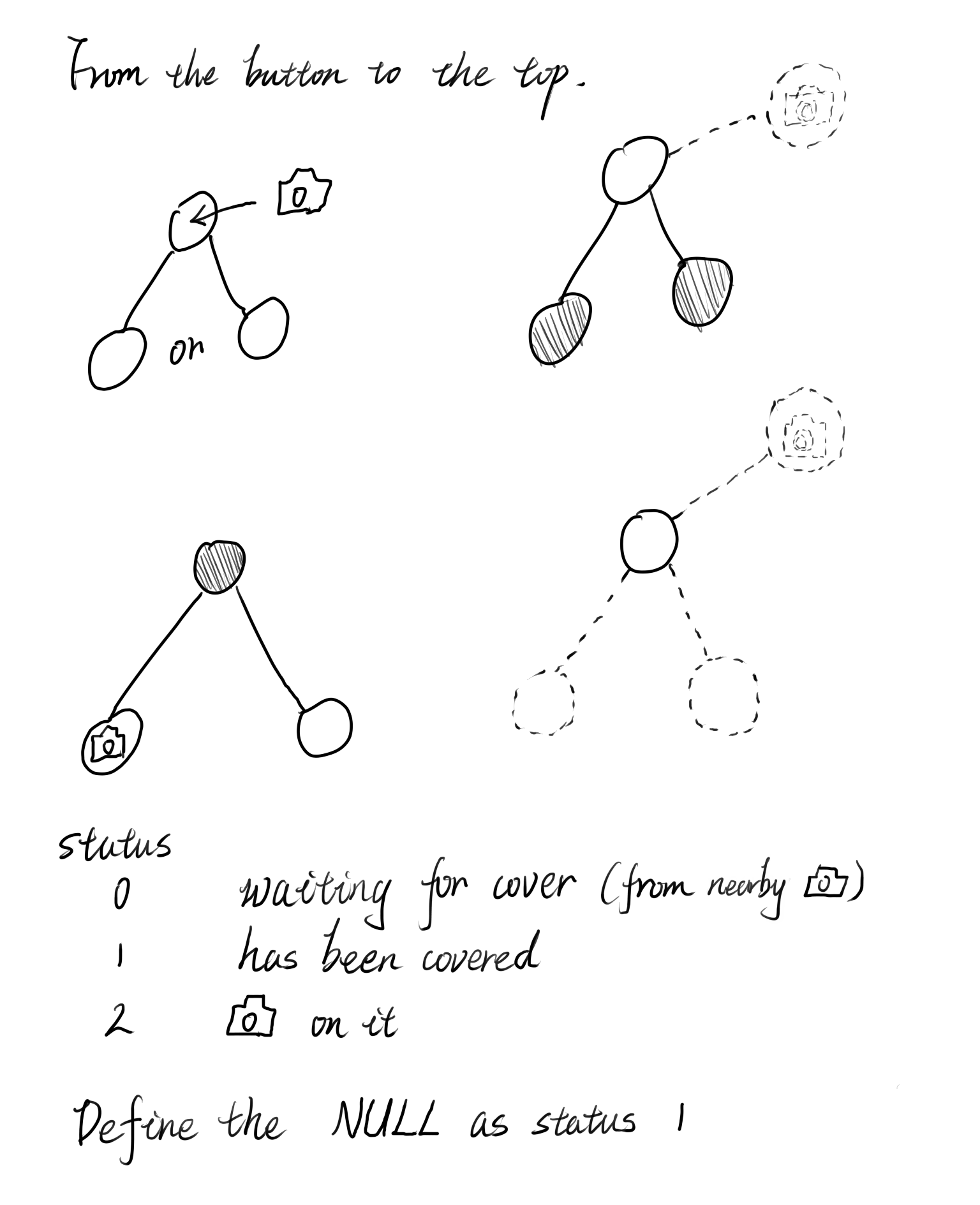

我们考虑有以下几种情况：

• 当一个结点的左或右子树没有被摄像头覆盖上时，这个结点必须要安装一个摄像头来监测其左或右子树，定义为状态码STATUS_CAMERA
• 当一个结点的左右子树都已经被摄像头覆盖上时，为了实现摄像头数量的最小化，需要在该结点的父结点放置摄像头，即在回到父结点前该结点都是未被覆盖的，定义为状态码STATUS_UNCOVERED
• 当一个结点的左右子树中存在摄像头，则该结点肯定是被覆盖了的，定义为状态码STATUS_COVERED
• 对于结点为NULL的情况，我们可以默认他是被覆盖了的结点，即定义为状态码STATUS_COVERED

同时，我们还需要对这棵树的根节点做一次单独的检测，以确定是否要在其上放置摄像头

为了方便判定，我们将STATUS_CAMERA设置为状态码中值相对大的一个

状态转移方程

STATUS_ROOT = F(STATUS_LEFT, STATUS_RIGHT)

时间复杂度：

n次遍历，线性时间复杂度O(N)

空间复杂度：

递归算法要开辟n个栈空间，故为线性空间复杂度O(N)

构造代码如下：

C语言版

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

/*
 * status code
 * 0: waiting for pwn
 * 1: has been pwn
 * 2: camara here
 *-1: inner error, just a placeholder in fact
 */
#define STATUS_UNCOVERED 0
#define STATUS_COVERED 1
#define STATUS_CAMERA 2
#define STATUS_ERROR -1

int minCameraCover(struct TreeNode* root) 
{
    int amounts=0;//amounts of camera

    //add a camera to the root if status of root is 0
    if(dfs(root,&amounts) == STATUS_UNCOVERED)
        amounts++;
    return amounts;
}

int dfs(struct TreeNode* root, int * amounts)
{
    //NULL pointer signed as status 1
    if(!root)
        return STATUS_COVERED;

    //get the status of left and right node
    int left = dfs(root->left, amounts);
    int right = dfs(root->right, amounts);

    //if one of both uncovered yet, a camera is needed
    if(left == STATUS_UNCOVERED || right == STATUS_UNCOVERED)
    {
        (*amounts)++;
        return STATUS_CAMERA;
    }

    //if both are covered, father's of root may need a camera
    if(left == STATUS_COVERED && right == STATUS_COVERED)
        return STATUS_UNCOVERED;
    
    //if there's at least one camera in both childs, the root is covered
    if(left + right > STATUS_CAMERA)
        return STATUS_COVERED;
    
    //error code(not used)
    return STATUS_ERROR;
}

Python语言版：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

#  status
#  0 - waiting for pwn
#  1 - has been pwn
#  2 - camera here
# -1 - error, just a placeholder

class Solution:
    amounts = 0

    def dfs(self, root: TreeNode) -> int:
        if root == None:
            return 1
        left = self.dfs(root.left)
        right = self.dfs(root.right)
        if left == 1 and right == 1:
            return 0
        if left == 0 or right == 0:
            self.amounts += 1
            return 2
        if left + right > 2:
            return 1
        return -1

    def minCameraCover(self, root: TreeNode) -> int:
        if self.dfs(root) == 0:
            self.amounts += 1
        return self.amounts