Leetcode - 685：冗余连接II

并查集并查集并查集…

685. 冗余连接 II（困难）

在本问题中，有根树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。每一个节点只有一个父节点，除了根节点没有父节点。

输入一个有向图，该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。 每一个边 的元素是一对 [u, v]，用以表示有向图中连接顶点 u 和顶点 v 的边，其中 u 是 v 的一个父节点。

返回一条能删除的边，使得剩下的图是有N个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1:

输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的有向图如下:
1
/
v v
2–>3
示例 2:

输入: [[1,2], [2,3], [3,4], [4,1], [1,5]]
输出: [4,1]
解释: 给定的有向图如下:
5 <- 1 -> 2
^ |
| v
4 <- 3
注意:

二维数组大小的在3到1000范围内。
二维数组中的每个整数在1到N之间，其中 N 是二维数组的大小。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/redundant-connection-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法：并查集

半夜三点多把前置题：684. 冗余连接给做了，感觉稍微有了点头绪，其实还是啥都不知道…

晚上大概想清楚了，同样是采用并查集的思想，不过考虑到该图为有向图，同时题目给定的图必定存在一条边使得该图无法成为一颗树

可能存在如下情况：

• 一个节点的入度大于等于2（存在两个及以上父结点，本题数据构造保证只可能存在两个父结点的情况）
• 图中存在回路
• 以上两种情况同时存在

如下图所示（字丑见谅QwQ）：

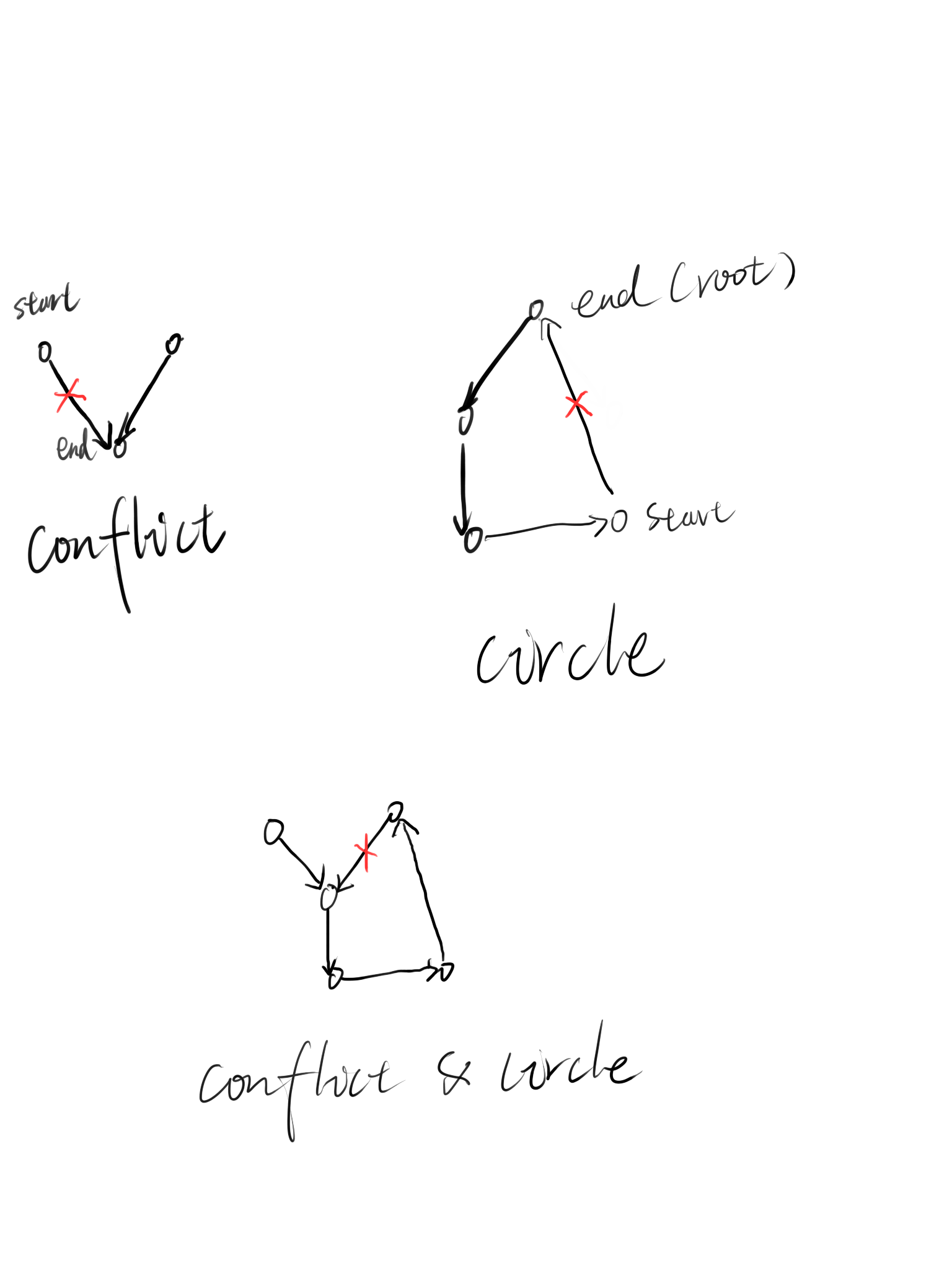
故我们很容易（并不Or2）能够得到解开这道题的算法：

• 将每一个结点初始化为一棵单独的树，其父结点初始化为自身
• 使用两个数组分别保存每个结点的父结点与所属的树的根结点
• 遍历每一条边，重新记录下每个结点的父结点与根节点
• 当一个结点的入度大于1时，记录该边为争议边
• 当一条边的始末结点同属于一棵树时，记录该条边为回路边
• 两种情况都不存在，则将该边的末结点的父结点标为该边的始结点，并合并两结点所在的树
• 当争议边不存在时，直接删除回路边
• 争议边若存在，若同时存在回路边，则删除争议边末尾结点及其父结点所构成边，否则删除争议边

构造代码如下：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 /**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int * ancestors;//记录每个节点的根结点
int * parent;//记录每个节点的父结点

int find_x(int x)
{
    return x == ancestors[x] ? x : (ancestors[x] = find_x(ancestors[x]));//路径压缩
}

void union_ancestor(int a, int b)
{
    ancestors[find_x(a)] = find_x(b);//将两棵树合并为一棵树
}

int* findRedundantDirectedConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize)
{    
    ancestors = (int*)malloc(sizeof(int)*(edgesSize+5));
    parent = (int*)malloc(sizeof(int)*(edgesSize+5));

    for(int i=1;i<=edgesSize;i++)
    {
        parent[i] = ancestors[i] = i;//初始化每个结点为单独的一棵树（并查集），结点的父结点标记为自身
    }
	//conflict：可能存在争议的边
    //circle：可能形成回路的边
    int start, end, a_start, a_end, conflict = -1, circle = -1;

    for(int i=0;i<edgesSize;i++)
    {
        start = edges[i][0];
        end = edges[i][1];
        a_start = find_x(start);
        a_end = find_x(end);
        if(parent[end] != end)//该条边的尾结点已经与其他结点相连（即加上这条边后入度大于1）
        {
            conflict = i;
        }
        else
        {
            parent[end] = start;
            if(a_start == a_end)
            {
                circle = i;//该条边两结点的根结点相同，可能形成回路
            }
            else
            {
                union_ancestor(start, end);//将两棵树合并为一棵树（并查集）
            }
        }
    }

    int *ret = (int*)malloc(sizeof(int)*2);
    *returnSize = 2;
    if(conflict<0)//不存在争议边，只存在形成回路的边
    {
        ret[0] = edges[circle][0];
        ret[1] = edges[circle][1];
        return ret;
    }
    else//存在争议边
    {
        if(circle>0)//同时存在回路边
        {
            ret[0] = parent[edges[conflict][1]];
            ret[1] = edges[conflict][1];
            return ret;
        }
        else
        {
            ret[0] = edges[conflict][0];
            ret[1] = edges[conflict][1];
            return ret;
        }
    }
    return ret;
}