GWCTF 2019 write up for xxor

z3是个坏家伙（x

惯例的拖入IDA进行分析

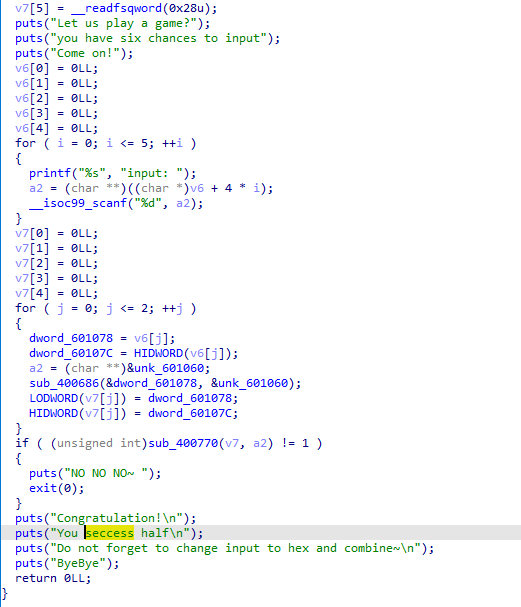
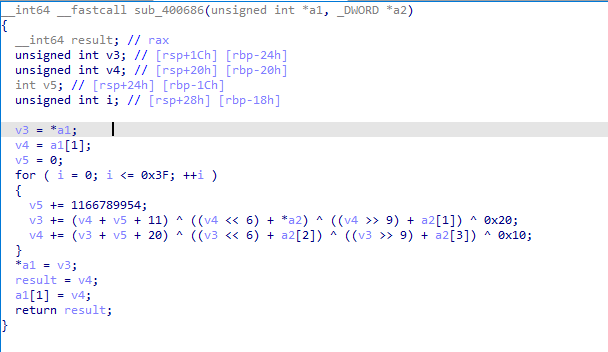
一开始先输入六个字符，之后是每两个字符放入sub_400686()中进行处理，跟进该函数

变量v3、v4分别为每组的第1、2个字符，在这里进行了十分令人作呕的算术操作（x

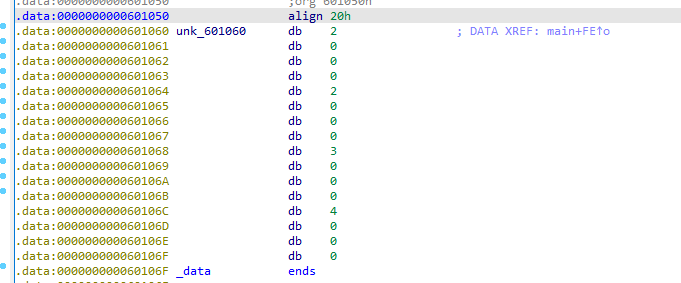
在这里所传入的参数a2为bss段上变量，按dword来读的话应该是一个数组[2, 2, 3, 4]（小端序）：

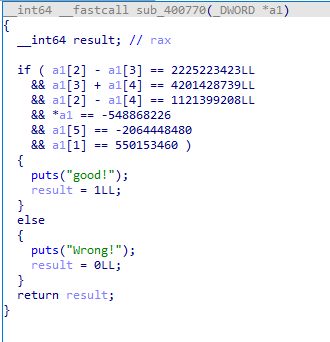
处理后进行flag验证的函数sub_400770()逻辑如下：

这里还需要解一个小方程得到a1[2]、a1[3]、a1[4]的值，用z3快速解方程：

这里z3在本地虚拟机安了没法用，在阿里云学生机上倒是能跑，离谱…

from z3 import *
x = [0] * 6
for i in range(6):
    x[i] = Int('x[' + str(i) + ']')

s = Solver()
s.add(x[0]==0xDF48EF7E)
s.add(x[5]==0x84F30420)
s.add(x[1]==0x20CAACF4)
s.add(x[2]-x[3]==0x84A236FF)
s.add(x[3]+x[4]==0xFA6CB703)
s.add(x[2]-x[4]==0x42D731A8)

s.check()
print(s.model())

$ python3 py.py 
[x[2] = 3774025685,
 x[3] = 1548802262,
 x[4] = 2652626477,
 x[1] = 550153460,
 x[5] = 2230518816,
 x[0] = 3746099070]

那么我们逆着这个逻辑就可以得到解密程序如下：

在这里没有用python的原因是源程序计算中必定发生整型溢出，而python普通的整型没有溢出

#include <iostream>
#include <cstdio>
using namespace std;
int main(void)
{
    unsigned int enc[6] = {3746099070, 550153460, 3774025685, 1548802262, 2652626477, 2230518816};
    int a2[4] = {2, 2, 3, 4};
    int val = 0x40 * 1166789954;
    for(int i=0; i< 6; i+=2)
    {
        int v5 = val;
        unsigned int v3 = enc[i], v4 = enc[i + 1];
        for(int j=0; j< 0x40; j++)
        {
            v4 -= (v3 + v5 + 20) ^ ((v3 << 6) + a2[2]) ^ ((v3 >> 9) + a2[3]) ^ 0x10;
            v3 -= (v4 + v5 + 11) ^ ((v4 << 6) + *a2) ^ ((v4 >> 9) + a2[1]) ^ 0x20;
            v5 -= 1166789954;
        }
        enc[i] = v3;
        enc[i + 1] = v4;
    }
    for(int i=0; i < 6; i++)
        printf("\'0x%x\', ", enc[i]);
}

最终解密脚本如下：

flag = ['0x666c61', '0x677b72', '0x655f69', '0x735f67', '0x726561', '0x74217d']
for i in flag:
    temp = i[2:]
    while temp != '':
        print(chr(int('0x' + temp[:2], 16)), end = '')
        temp = temp[2:]

得到flag：

flag{re_is_great!}